Estrategias de cálculo mental para primaria

Descomponer y dar saltos

Si piensas en cómo aprendiste a sumar o restar en el colegio, seguramente te venga a la cabeza una imagen parecida: números colocados en columna, reglas para “llevar” o “pedir prestado” y una repetición casi mecánica de pasos hasta que salía el resultado correcto.

Este enfoque, centrado en la memorización de algoritmos, fue útil para resolver operaciones, pero muchas veces no nos ayudó a entender del todo por qué hacíamos lo que hacíamos.

Hoy sabemos que existen otras formas de abordar el cálculo que no solo permiten llegar al mismo resultado, sino que lo hacen desde la comprensión. Dos de esas estrategias son la descomposición de números y los saltos en la línea numérica. Aunque no son nuevas, su aplicación práctica en la enseñanza de las matemáticas en primaria es relativamente reciente, y ofrecen una base mucho más sólida para construir aprendizajes posteriores.

En este artículo te explicamos cómo funcionan estas dos estrategias y qué materiales manipulativos puedes usar en casa para reforzar su comprensión. Son ideas sencillas, que puedes aplicar fácilmente, y que ayudan a los niños no solo a resolver operaciones, sino a entender mejor los números y confiar en su propio razonamiento.

Descomposición de números: partir del valor posicional

La descomposición consiste en dividir los números en partes más fáciles de manejar: normalmente, decenas y unidades. Es una estrategia útil tanto para sumar como para restar, y permite que el niño o la niña se apoye en el valor posicional, es decir, en entender que un 34 no es “tres-cuatro”, sino 30 y 4.

Véamoslo mejor con un ejemplo:

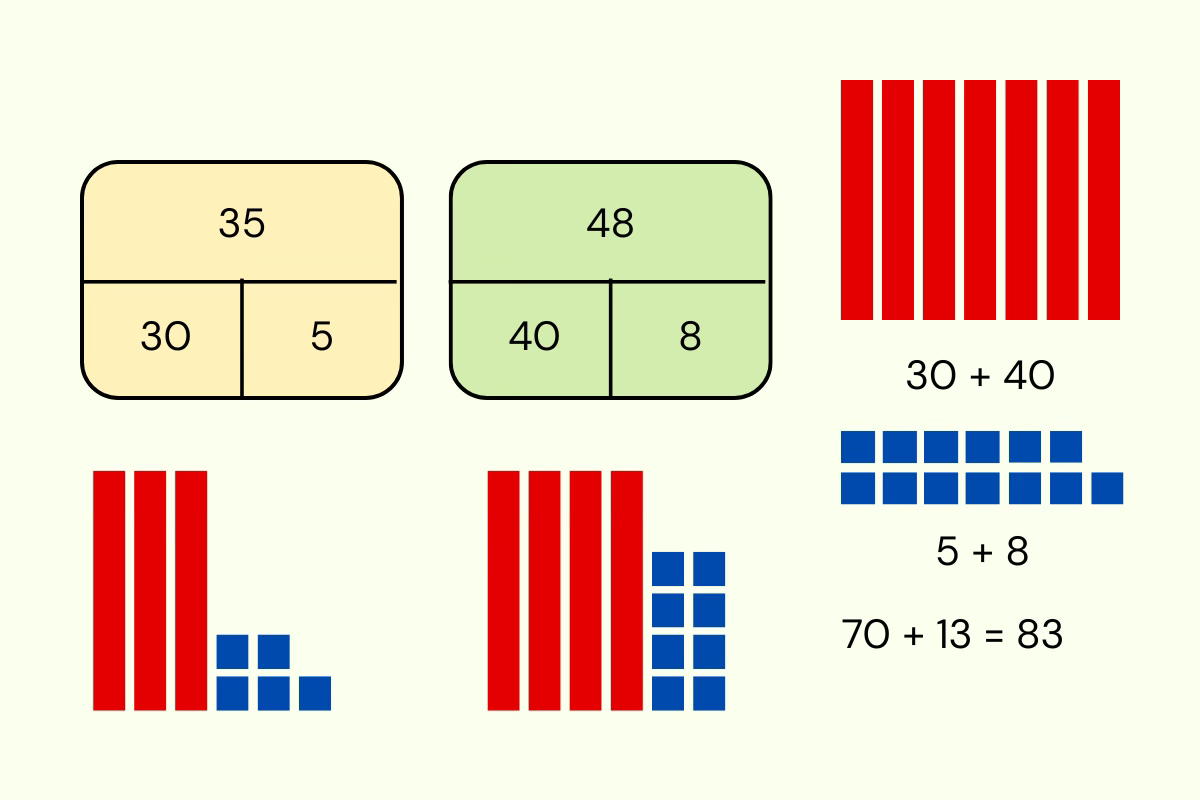
Imaginemos que queremos sumar 35 + 48. Estos son los pasos que podríamos seguir:

• Descomponemos 35 en 30 y 5

• Descomponemos 48 en 40 y 8

• Sumamos las decenas: 30 + 40 = 70

• Sumamos las unidades: 5 + 8 = 13

• Y por último: 70 + 13 = 83

Esta estrategia da pie a conversaciones matemáticas ricas, permite visualizar la operación en bloques y evita errores típicos como confundir la colocación de cifras al escribir en columna. Además, prepara el terreno para operaciones más complejas como la multiplicación o la división, donde la descomposición vuelve a ser clave.

Saltos en la línea numérica: avanzar paso a paso

En lugar de descomponer ambos números, esta estrategia propone mantener el mayor completo y descomponer solo el segundo. A partir de ahí, se realizan “saltos” en la línea numérica.

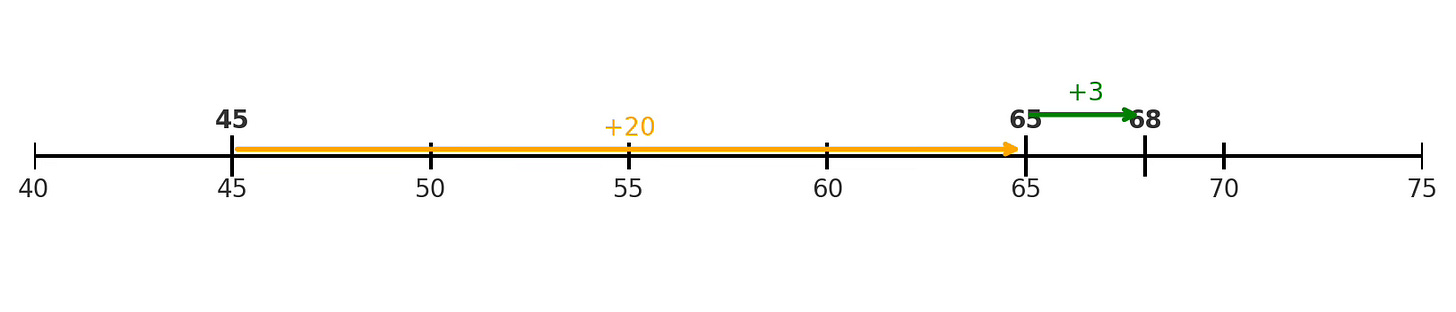
Ejemplo para sumar 45 + 23:

• Empezamos en 45

• Hacemos un salto de 20 → 65

• Hacemos un salto de 3 → 68

Esta forma de calcular es especialmente útil cuando los niños están empezando a dominar la línea numérica mentalmente. También permite entrenar la estimación y el cálculo rápido, algo fundamental cuando no se puede (ni conviene) depender de lápiz y papel o calculadora todo el tiempo.

Materiales manipulativos que acompañan

Ambas estrategias se entienden mejor si al principio se apoyan con materiales concretos:

Bloques base 10

Permiten visualizar claramente las decenas y las unidades. Se pueden usar para “construir” los números y operar con ellos físicamente. Este material lo asociamos a la estrategia de descomposición

Recuperemos el ejemplo que hemos empleado anteriormente en la descomposición para entender el funcionamiento:

Queremos sumar 35 + 48 utilizando bloques base 10.

Descomponemos cada número:

• 35 → 3 barras (decenas) y 5 cubitos (unidades)

• 48 → 4 barras (decenas) y 8 cubitos (unidades)

Los niños tienden de forma natural a agrupar barras con barras y cubitos con cubitos. Así que suman primero las decenas:
30 + 40 = 70,
y después las unidades:
5 + 8 = 13

Al ver que tienen más de 10 cubitos, reconocen que eso se puede convertir en una barra más, ya que vamos haciendo “paquetes” de cubitos que después pueden cambiar por una barra. Es decir, 13 = 10 + 3, y esa barra se suma a las que ya tenían:

60 + 10 + 3 = 73

De esta forma, no solo resuelven la operación, sino que comprenden de forma intuitiva cómo funciona el valor posicional y por qué “llevamos una” cuando usamos algoritmos tradicionales

Collares de bolas

Útil para introducir la estrategia de saltos. Se puede empezar contando hacia delante y hacia atrás de forma visual y manipulativa, marcando físicamente los saltos. Una vez interiorizada esta dinámica, se puede pasar a representar la línea numérica sobre papel, y más adelante, realizarla de forma mental sin necesidad de dibujarla.

Estos apoyos permiten que el niño pase de lo concreto a lo abstracto con seguridad. No es necesario usarlos durante mucho tiempo, pero sí al principio -tienen sentido sobretodo en los primeros años de primaria- para construir una base sólida.

Caminos distintos para llegar al mismo sitio

Estas dos estrategias no excluyen a los algoritmos tradicionales y ayudan a llegar a ellos desde la comprensión, en lugar de hacerlo desde la repetición. De la misma manera que existen varios caminos para llegar a un mismo destino, en matemáticas también hay distintas formas de resolver una operación.

Las estrategias de cálculo mental como la descomposición y los saltos forman parte del trabajo que proponemos en nuestras guías. Son una herramienta más dentro de un enfoque más amplio que busca sentar las bases de la comprensión numérica, el sentido del cálculo y la resolución de problemas desde los primeros cursos.

• La guía de primer curso (1º de Primaria) ya está disponible y cubre el inicio del cálculo mental, incluida la introducción a estas dos estrategias. La guía también abarca la introducción a la numeración, a las operaciones básicas y a la resolución de problemas.

• La guía de segundo curso (2º de Primaria) que publicaremos próximamente, dará continuidad a este trabajo, profundizando, entre otros temas, en la estructura del sistema decimal.